RALV
CAUSAL ANALYSIS
THE PRODUCT
RALV (Relationships Among Latent Variables) makes possible the implementation of stable and distortion-free causal analyses (structural equation models).
FEATURES IN BRIEF
- Analyzes effective relationships between latent variables
- Convenient graphical model construction
- Ability to play through many model variants quickly and securely without long familiarization or specialized methodological knowledge
- Orthogonalization as an effective solution for the avoidance of distortions in estimated path coefficients due to multicollinearity
- Uses the information from missing values to enhance the quality of the results
OBJECTIVE
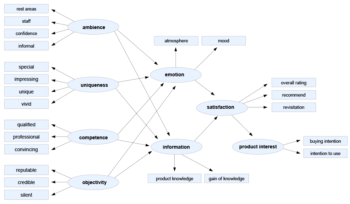
Structural Equation Modeling is used to inspect causal relationships between variables. The objective is to investigate hypothetical structures of correlations and influences. As with regression analysis, the analysis looks for the amount and direction of influence of one or more so-called exogenous variables on one or more endogenous variables.
As with factor analysis, the assumption is made that the attribute to be investigated cannot be observed directly, but rather “latently” represents the basis for the observed behavior, opinion or attitude expressed by the respondent. These latter observations serve as indicators for the level of the underlying basic attributes.
Structural equation models are initially based around a hypothesis stating which attributes are influenced by which variables. In this manner, complex covariance structures can be set up, whereby attributes can simultaneously be independent (influencing) and dependent (influenced by others). Structural equation models check this hypothesis by measuring the degree of the impact of the independent variables and determining the goodness of fit of such a model.
PREREQUISITES
Structural equation models cannot detect improperly assumed directions of relationship. The direction of the influence, or in other words, the question of whether feature A influences feature B or vice versa, must be established through preliminary theoretical consideration.
In order to be able to interpret the coefficients properly, the influencing variables of an endogenous variable should be mutually independent.
PRACTICAL IMPLEMENTATION
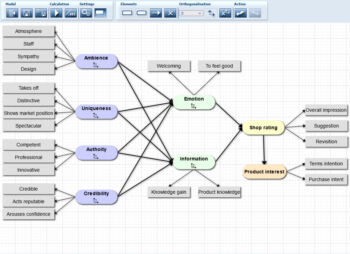
With RALV (Relationships Among Latent Variables), IfaD provides a tool for the realization of causal analyses, which like the classic structural equation modeling methods provides confirmatory analysis of linear relationships between latent variables.
RALV (Relationships Among Latent Variables) makes possible the implementation of stable and distortion-free causal analyses (structural equation models).
However it differs from existing approaches in two key respects, which facilitate the handling of typical characteristics of survey data: multicolinearity and missing values.
Inter-correlations between influencing variables of an endogenous variable lead to distortions in the calculated path coefficients. If this multicolinearity is ignored, the influence of the dominant variable is given too much weight. The influence of the remaining variables, which strongly correlate with it, is suppressed (suppression effect).
Through a special orthogonalization procedure, RALV can completely eliminate inter-correlations between influencing variables. For this, all the resulting principal components of a complete factor solution are used to depict the original variables. In this way, for each influencing variable a (new) latent variable is extracted which represents its unique core content. Overlaps with the remaining variables incorporated in the principal component analysis, and thus multicolinearity, are excluded. These new variables form the basis for the calculation of coefficients, which then become comparable and interpretable.
For various reasons answers of respondents regarding specific items can be are lacking. If their absence is a sign, that these items are not of importance to the respondent that fact can be considered as valuable information within the analysis. If the missing answers are replaced by mean of this item on the basis of the answers of the other respondents, the coefficient of these variables decreases due to the decreased variant. The more respondents don’t answer that question, meaning the bigger the proportion of the sample for which that aspect is insignificant, the more the coefficient decreases.
With RALV it is not only possible to make a plain mean substitution. It also makes it possible to take into account specifications for the number of available responses in each case, so that the calculation is only based on those respondents who gave responses to at least a predefined proportion of the variables in the overall model or in sub-models.
These two innovative approaches are integrated in RALV in a user-oriented way. With its assurance that the algorithm used always delivers robust model calculations without forced restrictions – even with small sample sizes – and with convenient graphical model construction, RALV represents an efficient tool for the market researcher. With this tool, causal analyses can be used without significant barriers and limitations.